朴素贝叶斯分类器

发表于 | | 阅读次数: |

因为工程实践里需要实现语义分析的功能，关于如何语义分析，我也是一头雾水。最近花了点时间，依据贝叶斯原理，针对工程实践，写了一个分类器，效果还阔以~~ 哈哈

写在前头

在研一上学期的时候，学院里分配了一个工程实践项目，我所在的4人组选了基于语义的搜索引擎这个课题，项目主页：https://github.com/willstudy/SearchEngine。目前项目进展到语义分析模块了，我就查阅了相关资料，然后根据项目的数据集，定制了一个贝叶斯分类器。

贝叶斯定理

老是说我第一眼看到这个定理的时候，完全没有任何印象。其实这个定理最早出现在本科所学的概率论中的，好惭愧，竟然被我忘光了。。。

贝叶斯定理主要是：当知道A发生的情况下，B发生的概率 P( B | A) 时， 求 B 发生的条件下，A发生的概率 P( A | B )，其公式为：

来自百度搜索

这个公式在生活很有用，我们在不知不觉中可能就用到了它。比如说，在街上看到一个黑种人，我们很自然的联想到，他可能来自非洲。在得出判断的过程中，我们就用到了贝叶斯分类器的思想。

贝叶斯分类器

在生活，经常会进行各种各样的分类，比如说文档归类、网页分类等，使用的分类方法称之为分类器。大多数分类器都是基于贝叶斯定理展开的，大致过程如下：

  • 确定需要分出的类别：Y1,Y2,Y3…
  • 对目标分类对象进行特征**(X1,X2,X3…)**提取
  • 计算这些特征的先验概率，即P(X1|Y1),P(X2|Y1),P(X1|Y2)…
  • 根据贝叶斯公式，计算待分类的后验概率，即P(Y1|X1,X2,X3…)

贝叶斯计算后验概率的公式如下：

来自博客园截图

这里我会根据工程实践中的数据集，进行一步步的分析。

数据集的描述

我的这个工程实践，是基于语义的搜索引擎，主要做关于美食做法方面的搜索。其所有的数据都是从美食天下网爬到的数据，在此给贵网站带来的不便，致以深深的歉意。其中每条记录主要包含如下字段：

菜的标题|网站的URL|菜的介绍|菜图片的URL|菜的食材|菜的类型|菜的做法步骤|菜的小窍门

大约共3.5W条记录。

分类器的原型

老师说过，软件工程的第一步是需求分析。那我第一步从需求分析写起。项目需要的分类器的需求描述如下：
用户输入一句话，比如：

1
西红柿炒鸡蛋

分类器能判断用户是想检索菜名类别、食材类别还是工艺类别。因为我选用的分词工具对这句话分割的结果如下：

1
西红柿 炒 鸡蛋

如果只是简单的字符串匹配，那么它很可能既属于菜名，又可能属于工艺，又可能属于食材。这时候就需要一个分类器，对分词的结果进行分类处理。

所以这个分类器的输入是：分词后的词组，输出是: 类别。

分类器的设计

根据上文中提到的贝叶斯分类器的设计步骤，我做了如下工作：

1、类别确定

分类器的类别： 菜名、食材、工艺

2、特征提取

我这里提取的特征，是对分词工具一些简单的修改，然后使用它分词之后的结果作为特征。比如
西红柿炒鸡蛋 的特征为 西红柿 炒 鸡蛋，而 排毒养颜的菜 的 特征为 排毒 养颜 菜

3、计算先验概率

这一步花了我很多时间，首先，我用python把之前爬到的3.5W条记录，再次处理了一下。利用python把每个字段对应的信息提取出来。比如说，我共提取了36924条菜名、食材、工艺，分别单独存放在 title.txt、material.txt、type.txt 中。

然后利用分词工具对上述三个文件 title.txt、material.txt、type.txt 再次处理了一下，把它们分割成词条，分别单独存放在了 splite_title.txt、splite_material.txt、splite_type.txt 中。

然后这一步比较简单，我利用Python统计，上述分割后的文件中词条的词频，然后分别除以每个类别的词条总数。用python处理 split_title.txt 文件描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#coding=utf-8
from __future__ import division
import os
import sys
import re

reload(sys)
sys.setdefaultencoding('utf-8')

words = []
dictory = {}
word_set = []
new_dict = {}

file_read = open('split_material.txt', 'r')
file_write = open('percent_material.txt', 'w+')

for line in file_read.readlines():
	line = line.strip('\n')
	words.append(line)

word_set = set(words)   # exclude these repeated keyWords
length = len(words)
print length

for item in word_set :
	dictory[item] = words.count(item) / length    
new_dict = sorted( dictory.iteritems(), key = lambda d:d[1], reverse = True ) # sort by value

for key,value in new_dict:
	file_write.write( key + ":" + str(value) )
	file_write.write( '\n' )

最后会生成 percent_title.txt percent_material.txt percent_type.txt 文件。
最后一步，我这三个概率文件归并在一起，形成最后的先验概率集合。用python描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#coding=utf-8
from __future__ import division
import os
import sys

reload(sys)
sys.setdefaultencoding('utf-8')

file_title = open('percent_title.txt', 'r')
file_material = open('percent_material.txt', 'r')
file_type = open('percent_type.txt', 'r')
file_gather = open('gather.txt', 'w+')

title_num = 123320
material_num = 292582
type_num = 495875

laplace_title = 1 / ( title_num * 2 )
laplace_material = 1 / ( material_num * 2 )
laplace_type = 1 / ( type_num * 2 )

dictory_title = {}
dictory_material = {}
dictory_type = {}

for line in file_title.readlines():

	line = line.strip('\n')
	result = line.split(':')
	dictory_title[result[0]] = result[1]

file_title.close()

for line in file_material.readlines():

	line = line.strip('\n')
	result = line.split(':')
	dictory_material[result[0]] = result[1]

file_material.close()

for line in file_type.readlines():

	line = line.strip('\n')
	result = line.split(':')
	dictory_type[result[0]] = result[1]

file_type.close()

dictory = {}

for key in dictory_title:

	percent = []

	if dictory.has_key( key ):
		pass
	else :
		percent.append(dictory_title[key])
		percent.append( str(laplace_material) )
		percent.append( str(laplace_type) )

		dictory[key] = percent

for key in dictory_material:

	percent = []

	if dictory.has_key(key):
		percent = dictory[key]
		percent[1] = dictory_material[key]
	else:
		percent.append( str(laplace_title) )
		percent.append(dictory_material[key])
		percent.append( str(laplace_type) )

	dictory[key] = percent

for key in dictory_type:

	percent = []

	if dictory.has_key( key ):
		percent = dictory[key]
		percent[2] = dictory_type[key]
	else:
		percent.append( str(laplace_title) )
		percent.append( str(laplace_material) )
		percent.append(dictory_type[key])

	dictory[key] = percent

for key in dictory:

	file_gather.write(key + ':')

	for item in dictory[key]:

		file_gather.write( item + ' ' )

	file_gather.write('\n')

file_gather.close()

**有一种情况需要特别说明：**当一个词条只出现在一个类别，在其他类别没有出现时，它的先验概率计算：

1
2
3
laplace_title = 1 / ( title_num * 2 )
laplace_material = 1 / ( material_num * 2 )
laplace_type = 1 / ( type_num * 2 )

没错，这就是我采用的Laplace平滑方法。

4、计算后验概率

利用贝叶斯公式，分别求出 菜名、食材、工艺的后验概率。这一步我用PHP语言写的，因为我们的分词工具是SCWS的PHP扩展，半推半就的使用PHP写出了这个分类器。其PHP语言描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
<?php
/*
 *  核心模块：基于贝叶斯公式，定制的一个分类器，经测试准度较高
 */
function gather( $str )
{
	chdir("./lib/nlp/db");

	$hand_read = fopen( "gather.txt", 'r' );

	if( !$hand_read )
	{
		exit("file gather.txt open failed!");
	}

	$gather_container = array();
	/* 初始化数据集 */
	while( !feof($hand_read) )
	{
		$buffer = fgets( $hand_read, 1024 );
		$buffer = trim( $buffer , "\n" );
		list( $name, $title_proba, $material_proba, $type_proba ) = split( '[ :]',$buffer );

		$temp = array();

		$temp['title'] = $title_proba;
		$temp['material'] = $material_proba;
		$temp['type'] = $type_proba;

		$gather_container[$name] = $temp;
	}
	/* 每个类型的总条数 */
	$title_num = 123320;
	$material_num = 292582;
	$type_num = 495875;

	$total = $title_num + $material_num + $type_num;
	/* 这里的比重暂时没想好,越小，说明权重越大 */
	/*
	$title_percent = $total / $title_num ;
	$material_percent = $total / $material_num ;
	$type_percent = $total / $type_num ;
	*/
	$title_percent = 0.3;
	$material_percent = 0.3;
	$type_percent = 0.4;

	$title = $title_percent;
	$material = $material_percent;
	$type = $type_percent;
	$base = 2.7183;

	$num = count( $str );

	for( $i = 0; $i < $num; $i++ )
	{
		$word = $str[$i];

		if( array_key_exists( $word, $gather_container ) )
		{
			$probe_title = $gather_container[$word]['title'];
			$probe_material = $gather_container[$word]['material'];
			$probe_type = $gather_container[$word]['type'];
		}
		else
		{
			$probe_title = 1 / ( $title_num * 2 ) ;
			$probe_material = 1 / ( $material_num * 2 ) ;
			$probe_type = 1 / ( $type_num * 2 ) ;
		}

		$title *= log( $probe_title , $base );
		$material *= log( $probe_material, $base );
		$type *= log( $probe_type, $base );
	}
	/* 值越小，说明越趋近某个分类 */
	$title = abs( $title );
	$material = abs( $material );
	$type = abs( $type );

	$result = array();

	$min_probe = min( $title, $material, $type );
	/* 如果概率相差不大，就可以加入此类型中 */
	if( $title / $min_probe <= 2 )
	{
		$result['title'] = $title;
	}
	if( $material / $min_probe <= 2 )
	{
		$result['material'] = $material;
	}
	if( $type / $min_probe <= 2 )
	{
		$result['type'] = $type;
	}

	fclose( $hand_read );

	return $result;
}
?>

具体做法把先验概率加载进内存，分别查出每个特征的先验概率 probe_title probe_material probe_type，然后根据每个类别的初始比重，进行连乘，分别求出每个类别的概率，描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
if( array_key_exists( $word, $gather_container ) )
{
  $probe_title = $gather_container[$word]['title'];
  $probe_material = $gather_container[$word]['material'];
  $probe_type = $gather_container[$word]['type'];
}
else
{
  $probe_title = 1 / ( $title_num * 2 ) ;
  $probe_material = 1 / ( $material_num * 2 ) ;
  $probe_type = 1 / ( $type_num * 2 ) ;
}

$title *= log( $probe_title , $base );
$material *= log( $probe_material, $base );
$type *= log( $probe_type, $base );

这个分类器遇到了一些问题，我会在下部分提出，并写下我的解决方法。

分类器存在的问题及我的解决方案

关于Laplace平滑

若一个特征词只出现在某个分类中，比如说 金玉满堂，它只出现在菜名中，正常的计算结果概率为：

金玉满堂: 6.48718780409e-05 0.00 0.00

这样的计算会使一旦出现这个词，其他种类的概率立马变成0了，因为与0相乘，结果为0。这大大的降低了分类器的准确性。

解决措施：将其他类没有出现该词条的概率设为 1 / ( 2 * 词条总数 )，也称为Laplace平滑。最后 金玉满堂 的先验概率如下：

金玉满堂:6.48718780409e-05 1.70892262682e-06 1.00831862869e-06

关于乘积指数下溢的情况

因为词条种类共仅92W条，所以有的词条概率很低，那么它们进行贝叶斯公式的相乘时，就会造成丢失精度的情况。这种情况下我效仿了一位博主的做法，先对先验概率进行取自然对数，然后进行相乘。

关于特征值之间的独立性

因为贝叶斯公式要求各个特征之间是相互独立的，也就是说 西红柿 炒 鸡蛋 它们之间是没有关系的。然而实际上是有关系，它们之间的关联度，很大程度上觉得了分类结果。这里我的优化措施是，对最后的分类概率再进行平滑，若之间的概率相差不超过2倍，我就多返回一个分类，这样在丢失精度的情况下，同时保证了语义分析。

写在最后

这个分类器难度在于，对实际问题的抽象。如果知道了哪些是我们需要的特征值，怎么计算先验概率，那么剩下的工作就是数据的处理了。这个贝叶斯分类器效果其实还不错，值越小，说明越接近某个分类。大部分情况下，能得出我想要的分类结果。如下图所示：

分类结果
分类结果
分类结果

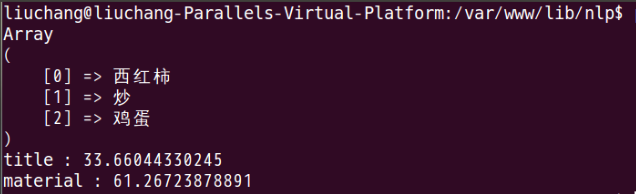
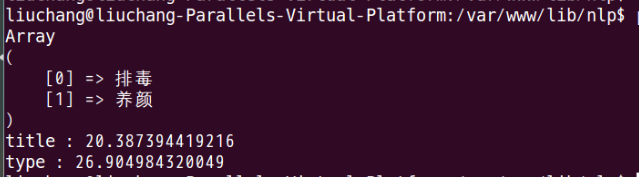
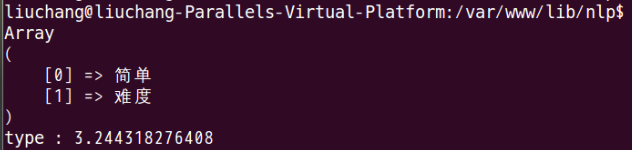
为了写这个分类器，连续写了3天代码，脸上长了几个痘痘。。。最后感谢那些提供我资料来源的博主们~~

参考

算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)
朴素贝叶斯分类及其在文本分类、垃圾邮件检测中的应用
Naive Bayes classifier