LDA在机器学习领域是一个应用很广泛的主题模型，这几天一直在学习这个模型，现在很勉强的对这个模型有了整体的把握，并且用Python简要的实现了一下，打算把自己对LDA的理解暂且记录一下，以后继续完善~

主题模型

LDA是一个主题模型，关于主题模型的解释有个很通俗的例子：

第一个是：“乔布斯离我们而去了。”
第二个是：“苹果价格会不会降？”

我们一眼就可以看出这两句是有关联的，第一句里面有了“乔布斯”，我们会很自然的把“苹果”理解为苹果公司的产品，它们属于了同一个主题：苹果公司。

而像我之前那种计算关联度的时候，即文档之间重复的词语越多越可能相似，是无法达到这个效果的。文档之间重复的词语越多越可能相似，这一点在实际中并不尽然。很多时候相关程度取决于背后的语义联系——主题描述，而非表面的词语重复。

LDA的与上述方法不同之处在于：上述方法直接处理单词与文章的关系，而LDA过程在单词与文章之间加了一层主题，即文档——主题，主题——单词的路径计算。

LDA的概要

很多关于介绍LDA的文章大多以学术、理科学生的思维出发的，即用数学公式的严谨性来推导整个LDA的过程。我看了好久才理清了这个流程，因为它涉及到的数学推导很多，很容易陷入公式推导的怪圈里，无法对整个LDA的思想有个整体把握。。。

JULY博主说LDA分为五个部分：

一个函数：gamma函数
四个分布：二项分布、多项分布、beta分布、Dirichlet分布
一个概念和一个理念：共轭先验和贝叶斯框架
两个模型：pLSA、LDA
一个采样：Gibbs采样

确实如此，如果要想完整的理清这个来龙去脉，上面五个部分是不可少的。现在我尝试逆推这个过程，即以工科生的思维来阐述，为什么LDA需要上述5个部分，即从Gibbs采样开始说起。

伟大的统计模拟

LDA模型的需求是什么呢？即得到文档——主题的概率分布，主题——单词的概率分步，这要怎么做呢？很直观的做法就是：

文档——主题：计算文档中属于Ki主题的单词数 / 文档单词总数
主题——单词：计算单词Wi属于Kj主题的单词数 / 属于Kj主题的单词总数

可问题是，对于一个文档集我们是很难知道每个单词对应的哪个主题的，那么上面的公式就无法计算，那这个问题如何解决呢？？这就要借助统计模拟过程了。

《LDA数学八卦》中把文章的创作过程形象的解释成上帝掷骰子的游戏，并在书中形象的阐述了几种模拟过程：Unigram Model，加上贝叶斯的Unigram Model，PLSA，加上贝叶斯的PLSA。下面我主要阐述一下这几个过程：

Unigram Model

最简单的Unigram Model认为上帝以下面这个规则来创作一篇文章：

1：上帝只有一个骰子，骰子有V个面，每个面代表一个单词，各个面的概率不一。
2：每抛一次骰子，抛出的面就对应这个单词。那么如果一篇文章有n个单词，那这篇文章就是上帝独立的抛了n次骰子的结果。

骰子各个面出现的概率定义为 P(p1, p2, p3, … , pv )，那么一篇文档 D(w1, w2, w3, … , wn ) 生成的概率就是

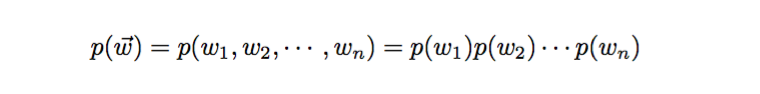
而文档与文档之间我们认为是独立的，所以如果有多篇文档 W(w1, w2, … , wm) 那么这个文档集的概率为：

假设文档集中单词总数为 N，我们关注每个单词 vi 的发生次数 ni，那么 n( n1, n2, … , nv )是一个多项式分布

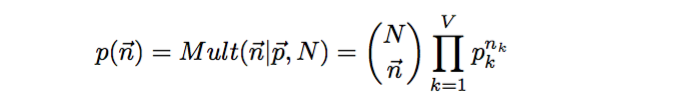
我们的任务就是通过这个模拟过程得到文档中单词的概率分布，也就是骰子每个面的概率是多大，那么可以通过最大似然使概率最大化，于是参数 pi 的值为

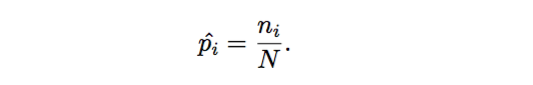
经过模拟过程，我们可以得到文档–单词的概率分步，即P(p1, p2, … , pv)。

关于最大似然的理解

假设有一个黑盒子，里面装满了五颜六色的小球。我们从这个盒子中随机的取出一个球记下颜色后，再放回盒子，重复这个动作100次。最后统计我们取出红色的个数，假如是80个，那么我们比较有把握确定黑盒子中红球的比例是80%左右，这个就是最大似然的概念。

加上贝叶斯的Unigram Model

贝叶斯学派认为上帝只有一个骰子是不合理的，他们认为上帝有无穷多的骰子，上帝以下面的规则创作一篇文章：

1：上帝有一个大坛子，里面装着很多骰子，每个骰子有V个面
2：上帝先从坛子里取出一个骰子，然后不断的抛，骰子抛出的结果就是创作了一篇文章

这与Unigram Model不同之处在于，上帝有很多骰子，这些骰子符合一个概率分布。那么在贝叶斯框架下，有如下关系：

1	先验概率 * 似然函数 = 后验概率

那么这里的骰子的先验概率如何选择呢？因为这个问题实际上是计算一个多项分布的概率，而Dirichlet分布恰好是多项分布的共轭分布。这里我们把骰子的先验概率看成Dirichlet分布。那么现在的贝叶斯框架就变成了

1	Dirichlet分布 * 多项分布的数据 = 后验分布为Dirichlet分布

在给定参数 p 的先验分布 Dir(p | a)的时候，各个词出现的概率为多项分布 n ~ Mult(n | p, N)，我们能很轻易的求出它的后验分布为 Dir( p | a+n )

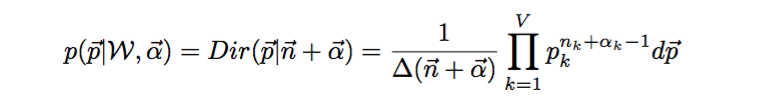
我们最主要的任务是估计筛子 V 个面的概率分布，由于我们有了参数的后验分布，所以合理的方式是使用后验分布的极大值点，或者参数在后验分布的平均值，在这里我们取平均值计算得到：

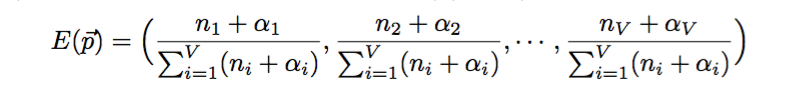
PLSA模型

前面2个都是铺垫，现在终于涉及到主题模型的统计模拟了。在PLSA(Probabilistic Latent Semantic Analysis)中，认为上帝是这么创作一篇文章的：

1：上帝有2种骰子，一种是doc-topic类型骰子，它有K个面，每个面对应一个文章主题。一种是topic-word骰子，总共K个，有V个面，每个面对应一个单词
2：上帝先抛doc-topic骰子得到一个主题编号Ki，然后选择第Ki个topic-word骰子进行抛掷，得到一个单词
3：假设这篇文章有n个单词，就重复上个过程n次

加上贝叶斯的PLSA

同Unigram Model类似，贝叶斯学派认为上帝的doc-topic和topic-word骰子要有先验概率分布的，即加上这2个Dirichlet先验概率分布最后成了我们的LDA模型。现在文章的创作过程变成了：

1：先随机抽取K个topic-word骰子，编号 1 到 K
2：在生成一篇新的文章时，先随机选择一个doc-topic骰子，再重复下面一个过程生成文章中的所有单词
3：投掷doc-topic骰子，得到主题编号 z，然后选择编号为 z 的topic-word骰子投掷，生成一个单词

那么文档到主题，主题到单词的概率分布如何计算呢？同加上先验的贝叶斯Unigram Model类似，文章——主题的概率计算如下：

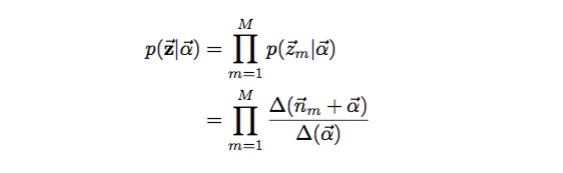
主题——单词的概率计算如下：

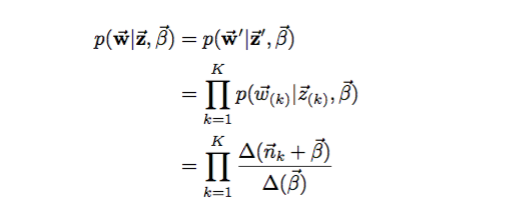
Nm表示第m篇文章的单词数，Nk表示第k个topic的单词数，Z向量表示主题分布，W向量表示主题——单词的分布。

注:
这里我省去了很多公式推导过程，大部分的推导，我自己还没看懂。。

公式里的alpha 和 beta被称为超参数，它们是Dirichlet分布中的参数。它们的作用解释如下：
alpha变小，是尽可能让同一个文档只有一个主题，beta变小，是让一个词尽可能属于同一个主题。

Gibbs sampling

现在整个模拟过程大致了解了，那么怎么让计算机来执行这个过程呢？Gibbs采样就是做这个过程的，但在正式叙述Gibbs采样之前，还得再加一个前戏，就是MCMC(Markov Chain Monte Carlo)。

马氏链

马氏链的数学定义比较简单

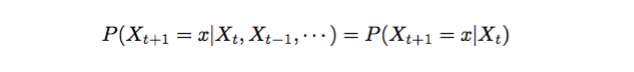
状态转移的概率只依赖前一个状态的概率。

它有一个很重要的性质：如果转移矩阵满足细致平稳条件的话，那么马氏链会最终收敛。它收敛的概率分布只依赖转移概率矩阵，与初始分布无关，这就很适合于给定概率分布的情况下，生成对应的样本。

注：

细致平稳条件：浅显的说，从状态A(x1, y1)转移到状态B(x1, y2)的概率 = 状态B(x1, y2)转移到状态A(x1, y1)的概率，如下所示：

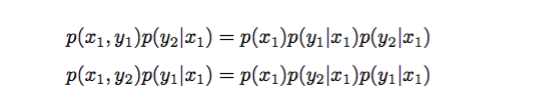
改造马氏链：MCMC

对于给定的概率分布p(x),我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布，于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,⋯xn,xn+1⋯,，如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本xn,xn+1⋯。

因为马氏链只有满足细致平稳的条件下，才会收敛，才能达到生成给定概率分布而对应的样本。在MCMC方法中，引入一个变量接受率alpha：

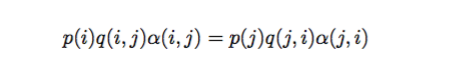
对于alpha怎样取值，才能使上面式子相等呢？最简单的，按照对称性，可以这样取值：

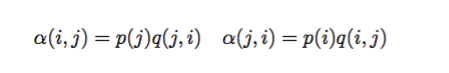
于是这样就可以满足细致平稳条件了

于是我们把原来具有转移矩阵Q的一个很普通的马氏链，改造为了具有转移矩阵Q′的马氏链，而 Q′恰好满足细致平稳条件，由此马氏链Q′的平稳分布就是p(x)！

由于接受率alpha有时候值太小，造成拒绝跳转，也就说很难收敛。这时候把**alpha(i,j)和alpha(j,i)**同比例放大，直到有一方达到1。对MCMC算法的接受率进行微小的改造，就得到了最常见的 Metropolis-Hastings 算法。

Gibbs抽样

Gibbs抽样跟MCMC过程很相似，不同之处在于：上述在放大alpha接受率的时候，可能很耗时。而Gibbs抽样可以很方便的做到使接受率达到1，即仅进行一维方向上的转移。例如有一个概率分布 p(x, y)，考察 x 坐标相同的两点 A(x1, y1) B(x1, y2)

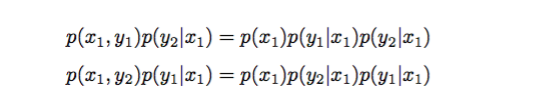
即

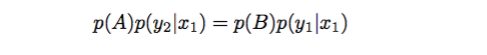
说明沿着坐标轴 x 的转移符合细致平稳条件，注意此时我们没有施加接受率这个参数，对于沿着坐标轴 y 轴情况也满足细致平稳条件。
那么Gibbs抽样在采样过程中，就会轮换着沿着x轴或者y轴进行转移。

文档中应用Gibbs抽样算法

由上述过程可以了解到，我们在知道文档的先验概率分布（Dirichlet分布）的情况下，Gibbs抽样是可以模拟文档生成的过程的。LDA的Gibbs抽样的公式推导的最终结果如下：

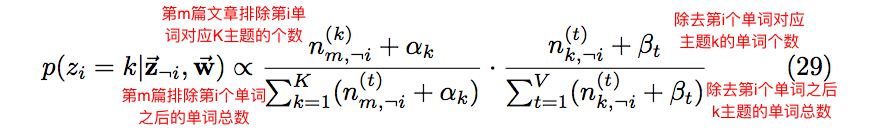
其算法如下：

1：因为马氏链的平稳状态与初始分布无关，这时候我们可以随机为每个单词 w 指定一个主题 z
2：重新扫描文档集，对每个单词以Gibbs sampling公式重新采样它的topic
3：重复上述过程，直到收敛为止
4：统计文档集中，doc-topic和topic-word的概率

小结

在学习LDA初期，我一直很疑惑这个模型输入的主题参数是什么？？其实就是一个文档集大致所包含的主题数目，超参数alpha和beta决定了文档——主题和主题——单词的先验概率，其规律大致如下：

1	alpha变小，是尽可能让同一个文档只有一个主题，beta变小，是让一个词尽可能属于同一个主题。

关于如何选择主题的个数以及超参数的设定，目前仍在学习过程中。。。

在JULY所说的五个过程还有gamma函数、二项分布、beta分布没有涉及，因为前面在提到先验概率时的多项分布，是从二项分布演化来的，这里我直接跳过去了。。而beta分布是二项分布的共轭分布，beta分布和二项分布的关系，与Dirichlet分布和多项分布的关系相似。

gamma函数是描述一个数的阶乘表示形式

它可以用来计算非整数的阶乘，因为二项分布、beta分布、多项分布、Dirichlet分布中，它们的概率计算公式可以使用gamma函数表示，在Gibbs sampling公式的推导过程中，把gamma消去了。所以为了整体把握LDA流程，这里我没有叙述这些知识

下一部分我决定写下我的LDA模型实现过程，以及模型的主题个数选择原则和模型的评价指标。

参考

[1] 《LDA数学八卦》
[2] CSDN JULY_通俗理解LDA
[3] 博客园 Entropy_主题模型解释
 [4] 博客园 ywl925_MCMC随机模拟