参考LDA数学八卦和GibbsLDA++实现的LDA模型,以及自己对这个模型的理解
LDA的Gibbs抽样
在上一篇文章中提到了Gibbs抽样的推导最终结果,根据这个推导公式可以在计算机上模拟文档集的生成过程。Gibbs抽样的推导结果如下:
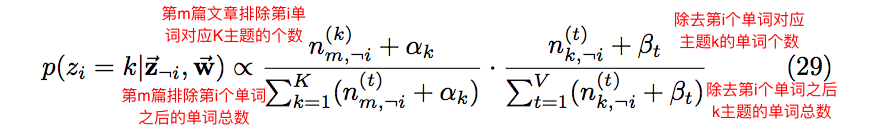
实现思路:
1:先随机为每个单词赋予一个主题
2:根据抽样公式计算当前单词生成每个主题的概率
3:利用掷骰子算法生成下一个主题
4:一直迭代下去,最后计算文档——主题、主题——单词的概率分布
代码放在了Github - LDA上了
数据结构的设计
根据抽样公式公式可知,需要保存的东西有
1:每个主题对应单词的个数
2:每个单词对应某个主题的单词个数
3:每篇文章单词的个数
4:每篇文章的每个主题对应的单词总数
用Python定义的数据结构如下:
1 | # 单词到ID的映射表 |
抽样过程
初始化
首先解析样本文件,随机为每个单词指定一个主题
1 | """ |
掷骰子算法
利用上述的抽样公式计算当前单词生成每个主题对应概率数组,在借鉴了GibbsLDA++的实现如下
1 | def sampling( self, doc_id, word_index ): |
把对应生成每个主题的概率计算出来之后,在计算机中如何生成指定概率分布条件下的样本值呢?掷骰子算法(像极了轮盘赌算法)的做法如下:
1 | """ |
文档——主题、主题——单词概率分布的计算
最后在再分别计算文档——主题、主题单词的概率分布
1 | def compute_theta( self ): |
LDA的推断过程
这里我是用PHP实现的,因为工程实践的服务器采用的编程语言是PHP。推断过程也是类似,不断这里需要辅助列表来保存新的样本集合,最终的目的还是计算新来的单词生成对应的每个主题的概率,然后利用掷骰子算法选择命中的主题。不断的迭代这个过程,使主题的分布趋于稳定。
1 | public function sampling( $index ) |
这里需要注意的是:样本集很少的情况下,那么在训练好的模型中很可能无法找到新来的待推断的单词,我的做法就是直接返回-1,也就是忽略了这篇文章中的这个单词。。。
代码放在了Github - SearchEngine上了
思考和感悟
我之前的想法是:
计算每篇文章的主题分布,然后利用计算好的模型推断出用户输入集合的主题分布,根据主题分布的相似性来判断用户在查找哪篇文章。
但实际编码出来之后的效果很不好,
一方面由于文档集中太多无关紧要的单词参与到整个抽样过程,可选的方法有只选文档中的名词或者形容词进行抽样。
一方面可能由于文档集规模很小的缘故,掷骰子算法还是不可避免的产生抖动,也就是说它不能像马尔科夫链那样最终收敛。
还有一方面主题分布之间的相似性度量我选择的是欧式距离,这样的度量在美食文章领域是否准确呢?