平衡二叉树

本文简要的实现了平衡二叉树的插入、删除操作。为了更新节点的平衡度，新增了parent指针。

简介

这个平衡二叉树使用C语言实现的，因为写的匆忙，加上智商捉急，可能某些地方没有考虑周全，会有一点小bug，尚在排查中。本算法能基本的实现平衡二叉树的插入、删除操作，有关平衡二叉树的原理及实现，参考AVL树(一)之 图文解析 和 C语言的实现。这位博主讲解的非常详细！！虽然他给的代码中有一些错误，但从他的博文中，我受益良多，并且重写了这个AVL树，在此表示感谢 ^_ .

数据结构

这里的parent指针很重要，它可以在平衡二叉树删除算法的调整过程中，起着很大的作用。有一点需要注明的是，那位博主的删除算法有误，选用的数据结构也不太合理。。

typedef int DataType;

typedef struct Node {
         DataType value;
         int depth;      // 保存节点在树中的深度，没有孩子，深度为1，负责深度为左右孩子最大深度值加1
         struct Node * left;
         struct Node * right;
         struct Node * parent;
} Node, *Tree;

基本思想

插入过程
我就不想说了，无非LL、LR、RL、RR型的旋转操作。想在这里记录一下：

删除算法的过程

1、若该节点有左右孩子
那么就用它的后继孩子节点替换该节点。假如本来删除的节点为node,它的左右孩子均非空，这时就用它的后继节点successor作为要删除的节点，即将successor节点的值赋给node，再删掉successor节点，因为这样需要调整的节点会少。

2、若该节点只有1个或0个孩子
直接删掉它。

关于调整过程：
对删除节点的父节点开始调整，更新其depth，并且向根节点开始迭代。计算每个父节点的左右子树的平衡差diff_depth，若为2则启动调整算法。

调整算法

基于四个调整操作，即LL、LR、RL、RR旋转。具体怎么旋转，参见那篇博文，灰常详细。

平衡二叉树C实现

#include <stdio.h>
#include <stdlib.h>

typedef int DataType;

typedef struct Node {
  DataType value;
  int depth;              // the position in this tree
  struct Node * left;
  struct Node * right;
  struct Node * parent;
} Node, *Tree;

int get_depth(Node * node) {
  if(node == NULL) {
    return 0;
  } else if(node->left == NULL && node ->right == NULL) {
    return 1;
  } else if(node->left == NULL && node->right != NULL) {
    return (node->right->depth + 1);
  } else if(node->left != NULL && node ->right == NULL) {
    return ( node->left->depth + 1 );
  } else {
    return (max( node->left->depth, node->right->depth ) + 1) ;
  }
}

int diff_depth( Tree T ) {
  if(T->left == NULL && T->right != NULL) {
    return T->right->depth;
  }
  else if(T->left != NULL && T->right == NULL) {
    return T->left->depth;
  }
  else if(T->left == NULL && T->right == NULL) {
    return 0;
  } else {
    if(T->left->depth > T->right->depth) {
      return T->left->depth - T->right->    depth;
    } else {
      return T->right->depth - T->left->depth;
    }
 }
}

int max(int a, int b) {
 return a > b ? a:b;
}

Node * get_node(Tree T, DataType value) {
  while(T != NULL) {
          if(value == T->value) {
            return T;
          }
          if(value > T->value) {
            T = T->right;
          } else {
            T = T->left;
          }
  }
  printf("get_node : not find this node < value : %d >\n", value );
  return NULL;
}

Node * get_successor(Tree T, Node * x) {
  if(x->right != NULL) {
      Node * p = x->right;
      while ( p->left != NULL ) {
              p = p->left;
      }
      return p;
  } else {
      Node * parent = x->parent;
      while ( parent != NULL && x->value > parent->value ) {
              parent = parent->parent;
      }
      return parent;
  }
}

Tree left_left_rotate(Tree T) {
  Node * node;

  node = T->left;
  node->parent = T->parent;
  T->left = node->right;
  T->parent = node;
  node->right = T;

  T->depth = get_depth( T );
  node->depth = get_depth( node );

  return node;    // new root node
}

Tree right_right_rotate(Tree T) {
  Node * node;

  node = T->right;
  node->parent = T->parent;
  T->right = node->left;
  T->parent = node;
  node->left = T;

  T->depth = get_depth( T );
  node->depth = get_depth( node );

  return node;    // new root node
}

Tree left_right_rotate(Tree T) {
  T->left = right_right_rotate( T->left );
  return left_left_rotate( T );
}

Tree right_left_rotate(Tree T) {
  T->right = left_left_rotate( T->right );
  return right_right_rotate( T );
}

Tree insert_fix_up(Node * node) {
  Node * father = node->parent;
  Node * temp_node = NULL;
  Node * root = NULL;

  if (father == NULL) return node ;
  if (father->parent == NULL) return father;
  while (father->parent != NULL) {
      if (diff_depth( father->parent ) == 2) {
          temp_node = father->parent->parent;
          if(father == father->parent->left) {
              if (node == node->parent->left) {
                  if ( temp_node == NULL ) left_left_rotate( father->parent );
                  else temp_node->left = left_left_rotate( father->parent );      // LL 调整
              } else {
                  if ( temp_node == NULL ) left_right_rotate( father->parent );
                  else temp_node->left = left_right_rotate( father->parent );             // LR 调整
              }
          }
          else {      // 在右子树中调整
              if ( node == node->parent->left ) {
                  if ( temp_node == NULL ) right_left_rotate( father->parent );
                  temp_node->right = right_left_rotate( father->parent );   // RL 调整
              }
              else {
                  if ( temp_node == NULL ) right_right_rotate( father->parent );
                  else temp_node->right = right_right_rotate( father->parent );   // RR 调整
              }
      }
      break;
    }
      father = father->parent;
      node = node->parent;
  }
  while ( temp_node != NULL ) {            //  更新调整后的深度
      temp_node->depth = get_depth( temp_node );
      temp_node = temp_node->parent;
  }
  root = node ;      // 从新插入的节点往上找root节点
  while( root->parent != NULL )
      root = root->parent;
  return root ;
}

Tree insert_node( Tree * T, DataType value )
{
        Node * parent = *T ;
        Node * node = NULL ;

        if( *T == NULL )
        {
                *T = ( Tree )malloc( sizeof( Node ) );

                if( *T == NULL )
                {
                        printf(" insert_node : error to create a node < value : %d >\n", value );

                        return *T ;
                }

                (*T)->left = NULL;
                (*T)->right = NULL;
                (*T)->depth = 1;
                (*T)->parent = NULL;
                (*T)->value = value;

                return *T ;
        }

        while( *T != NULL )
        {
                parent = *T;           // 得到要插入节点的父节点位置

                if ( value > (*T)->value ) *T = (*T)->right;

                else if ( value < (*T)->value ) *T = (*T)->left;

                else
                {
                        printf(" this Node: < value = %d > has existed!\n ", value );
                        return *T ;
                }
        }

        node = ( Node * )malloc( sizeof( Node ) );

        if( node == NULL )
        {
                printf(" insert_node : error to create a node < value : %d >\n", value );

                return *T ;
        }

        if ( value > parent->value )
        {
                parent->right = node;
        }
        else
        {
                parent->left = node;
        }

        node->left = NULL;
        node->right = NULL;
        node->parent = parent;
        node->depth = 1;
        node->value = value;

        while( parent != NULL )
        {
                parent->depth = get_depth( parent );
                parent = parent->parent;
        }


        *T = insert_fix_up( node );

        return *T ;
}

Tree delete_fix_up( Node * node )
{
        Node * child = NULL;

        if ( node->left != NULL )
        {
                child = node->left;

                if ( child->left != NULL )   // LL型调整
                {
                        return left_left_rotate( node );
                }
                else    // LR型调整
                {
                        return left_right_rotate( node );
                }
        }
        else
        {
                child = node->right;

                if ( child->left != NULL )   // RL型调整
                {
                        return right_left_rotate( node );
                }
                else    // RR型调整
                {
                        return right_right_rotate( node );
                }
        }
}

Tree delete_node( Tree * T, DataType value )
{
        Node * node = NULL;
        Node * delete_node = NULL;
        Node * father = NULL;

        if ( *T == NULL )
        {
                printf("Tree is NULL !!\n");
                return NULL;
        }

        node = get_node( *T, value );

        if ( node->left != NULL && node->right != NULL )
        {
                delete_node = get_successor( *T, node );     // 用被删的后继节点取代要删的节点

                node->value = delete_node->value;

                if ( delete_node->parent == node )    //后继节点就是它的右孩子，因为它的右子树没有左孩子
                {
                        if ( delete_node->right != NULL )
                        {
                                node->right = delete_node->right;
                                delete_node->right->parent = node;
                        }
                        else
                        {
                                node->right = NULL;
                        }

                        //node->depth = get_depth( node );
                }
                else      // 右子树有左孩子,一定是叶子节点，直接删掉
                {
                        delete_node->parent->left = NULL;
                }
        }
        else       //  要删除的节点只要一个字节点，或者没有字节点的情况
        {
                delete_node = node;
                father = delete_node->parent;

                if ( father != NULL )
                {
                        if ( father->left == delete_node )     // 在父节点的左子树上
                        {
                                if ( delete_node->left != NULL )   // 被删节点有左孩子
                                {
                                        father->left = delete_node->left;
                                        delete_node->left->parent = father;
                                }
                                else if ( delete_node->right != NULL )
                                {
                                        father->left = delete_node->right;
                                        delete_node->right->parent = father;
                                }
                                else
                                {
                                        father->left = NULL;
                                }
                        }
                        else     // 在父节点的右子树上
                        {
                                if ( delete_node->left != NULL )
                                {
                                        father->right = delete_node->left;
                                        delete_node->left->parent = father;
                                }
                                else if ( delete_node->right != NULL )
                                {
                                        father->right = delete_node->right;
                                        delete_node->right->parent = father;
                                }
                                else
                                {
                                        father->right = NULL;
                                }
                        }
                }
                else   // delete_node的父节点位NULL，说明此时删除的是根节点，又因为delete_node == node说明此时根节点只有一个子节点
                {
                        if ( delete_node->left != NULL )
                        {
                                *T = delete_node->left;
                        }
                        else if ( delete_node->right != NULL )
                        {
                                *T = delete_node->right;
                        }
                        else
                        {
                                *T = NULL;
                        }

                        goto end;
                }
        }


        father = delete_node->parent;    // 从这里开始，需要重新计算深度

        while( father != NULL )
        {
                *T = father;
                father->depth = get_depth( father );

                if ( diff_depth( father ) == 2 )
                {
                        Node * temp = father->parent;

                        if ( temp != NULL )
                        {
                                if ( temp->left == father )
                                {
                                        temp->left = delete_fix_up( father );
                                }
                                else
                                {
                                        temp->right = delete_fix_up( father );
                                }

                                father = temp;    // 继续向上调整
                                continue;
                        }
                        else
                        {
                                *T = delete_fix_up( father );   // 已调整到最上层
                                break;
                        }
                }

                father = father->parent;
        }

end:
        free( delete_node );

        return *T;
}

void mid_traversal( Tree T )
{
        if( T != NULL )
        {
                mid_traversal( T->left );

                printf(" value : %d , depth : %d \n", T->value, T->depth );

                mid_traversal( T->right );
        }
}

int main()
{
        Tree T = NULL;

        insert_node( &T, 3 );
        insert_node( &T, 2 );
        insert_node( &T, 1 );
        insert_node( &T, 4 );
        insert_node( &T, 5 );
        insert_node( &T, 6 );
        insert_node( &T, 7 );

        printf("------------orignal binary tree : --------\n");
        mid_traversal( T );
#if 1
        printf("\n-------delete node < value : %d >\n", 7 );
        delete_node( &T, 7 );
        mid_traversal( T );

        printf("\n-------delete node < value : %d >\n", 6 );
        delete_node( &T, 6 );
        mid_traversal( T );

        printf("\n-------delete node < value : %d >\n", 5 );
        delete_node( &T, 5 );
        mid_traversal( T );

        printf("\n-------delete node < value : %d >\n", 4 );
        delete_node( &T, 4 );
        mid_traversal( T );

        printf("\n-------delete node < value : %d >\n", 3 );
        delete_node( &T, 3 );
        mid_traversal( T );

        printf("\n-------delete node < value : %d >\n", 2 );
        delete_node( &T, 2 );
        mid_traversal( T );

#endif
        printf("\n------------ over -------------------\n");

        return 0;
}

运行结果

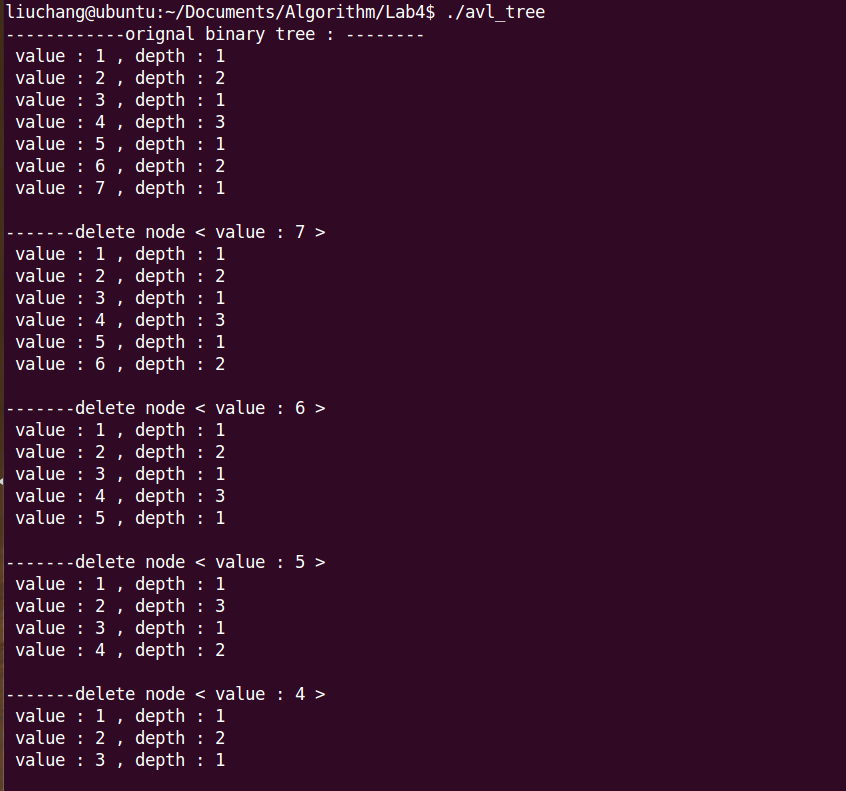
总结

理论与实践结合真的很重要，从书本上看这些算法没什么难的，自己动手写了一遍却被虐成了狗，同时也深深的敬佩提出这些算法的大牛们，佩服遇到问题时这么巧妙、这么机智的解决。

还有一点是，在于指针打交道的过程中，遇到段错误真是再平常也不过了。GDB真是一个你用了就会爱上它的好东西，解决段错误真是一大利器 ^_ 。