本文参考算法导论书籍以及一些博客,实现了红黑树的插入删除算法。
简介
红黑树这个算法,以后可能会再次遇到,我就在此记录一下。这个算法使用的C语言实现的。
红黑树的原理讲解
我是通过参考枫叶博主关于对红黑树讲解,以及算法导论这本书大致了解了红黑树的实现细节。具体参见红黑树删除操作。
红黑树的C实现
1 |
|
运行效果
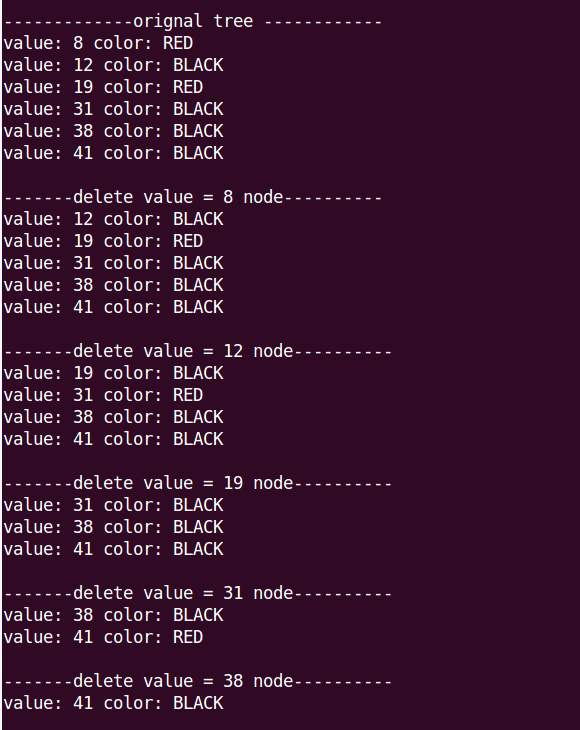
最后
这个算法写的比较仓促,没有考虑优化方面的事情。这个算法是参考这位博主,虽然他写的中有一些错误,但给我提供许多思路。再次感谢以上两位博主。
本文参考算法导论书籍以及一些博客,实现了红黑树的插入删除算法。
红黑树这个算法,以后可能会再次遇到,我就在此记录一下。这个算法使用的C语言实现的。
我是通过参考枫叶博主关于对红黑树讲解,以及算法导论这本书大致了解了红黑树的实现细节。具体参见红黑树删除操作。
1 | #include <stdio.h> |

这个算法写的比较仓促,没有考虑优化方面的事情。这个算法是参考这位博主,虽然他写的中有一些错误,但给我提供许多思路。再次感谢以上两位博主。